23. Vector Product(Cross Product)
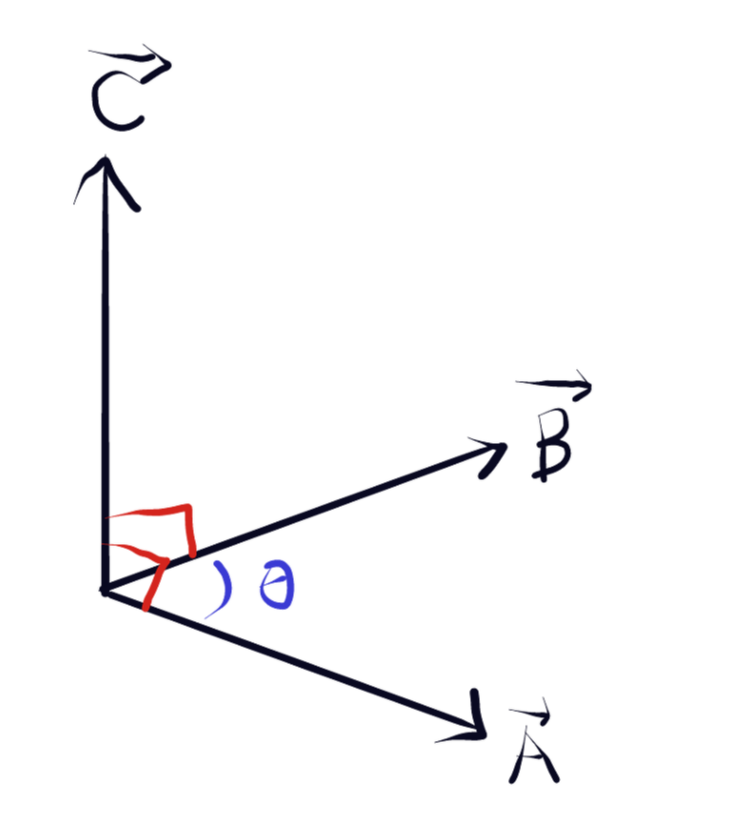
$ \vec{C}=\vec{A}\times \vec{B} $
$ C_{i}=\sum_{j,k}^{}\epsilon_{ijk}A_{j}B_{k} $
Levi-Civita Density(Permutation Symbol): $ \epsilon_{ijk}=\left\{\begin{matrix}
0 \\ +1
\\ -1
\end{matrix}\right. $
0: two or three indexes are same ($ \epsilon_{112},\epsilon_{113},\epsilon_{121},\epsilon_{131},\epsilon_{211},\epsilon_{311} $)
($ \epsilon_{221},\epsilon_{223},\epsilon_{212},\epsilon_{232},\epsilon_{122},\epsilon_{322} $)
($ \epsilon_{331},\epsilon_{332},\epsilon_{313},\epsilon_{323},\epsilon_{133},\epsilon_{233} $)
($ \epsilon_{111},\epsilon_{222},\epsilon_{333} $)
+1: i,j,k even permutation ($ \epsilon_{123},\epsilon_{231},\epsilon_{312} $)
-1: i,j,k odd permutation ($ \epsilon_{321},\epsilon_{213},\epsilon_{132} $)
$ C_{1}=\sum_{j,k}^{}\epsilon_{1jk}A_{j}B_{k}=\epsilon_{123}A_{2}B_{3}+\epsilon_{132}A_{3}B_{2}=A_{2}B_{3}-A_{3}B_{2} $
$ C_{2}=\sum_{j,k}^{}\epsilon_{2jk}A_{j}B_{k}=\epsilon_{213}A_{1}B_{3}+\epsilon_{231}A_{3}B_{1}=-A_{1}B_{3}+A_{3}B_{1} $
$ C_{3}=\sum_{j,k}^{}\epsilon_{3jk}A_{j}B_{k}=\epsilon_{312}A_{1}B_{2}+\epsilon_{321}A_{2}B_{1}=A_{1}B_{2}-A_{2}B_{1} $
$ \sum_{k}^{}\epsilon _{ijk}\epsilon _{lmk}=\delta _{il}\delta _{jm}-\delta _{im}\delta _{jl} $
$ (AB\sin \Theta )^{2}=A^{2}B^{2}(1-\cos^{2} \Theta)=(\sum_{i}^{}A_{i}^{2})(\sum_{i}^{}B_{i}^{2})-(\sum_{i}^{}A_{i}B_{i})^{2} $
$ =(A_{2}B_{3}-A_{3}B_{2})^{2}+(A_{3}B_{1}-A_{1}B_{3})^{2}+(A_{1}B_{2}-A_{2}B_{1})^{2} $
$ (AB\sin \Theta )^{2}=C_{1}^{2}+C_{2}^{2}+C_{3}^{2}=|\vec{C}|^{2}=C^{2} $
$ \Rightarrow C=AB\sin \Theta $
24. Result of Vector Product is Vector
$ \vec{A}\cdot (\vec{B}\times \vec{D})=\sum_{i,j,k}^{}\epsilon _{ijk}A_{i}B_{j}D_{k} $
$ \vec{D}\cdot (\vec{A}\times \vec{B})=\sum_{i,j,k}^{}\epsilon _{ijk}D_{i}A_{j}B_{k}=\sum_{i,j,k}^{}\epsilon _{jki}D_{i}A_{j}B_{k} $
$ \Rightarrow \vec{A}\cdot (\vec{B}\times \vec{D})=\vec{D}\cdot (\vec{A}\times \vec{B}) $ (i,j,k are dummy and can be renamed)
if $ \vec{A}=\vec{B} $ then $ \vec{A}\cdot (\vec{A}\times \vec{D})=\vec{D}\cdot (\vec{A}\times \vec{A})=\vec{D}\cdot 0=0 $
$ \Rightarrow \vec{A}, \vec{A}\times \vec{D} $ are perpendicular
$ \Rightarrow \vec{C}=\vec{A}\times \vec{B} $ is perpendicular to $ \vec{A},\vec{B} $(plane defined by $ \vec{A},\vec{B} $)
Direction of $ \vec{C} $: Right Hand Screw from $ \vec{A} $ to $ \vec{B} $
25. Vector Product of Unit Vector

$ \hat{e_{i}}\times \hat{e_{j}}=\hat{e_{k}}=\sum_{k}^{}\hat{e_{k}}\epsilon_{ijk} $ (i,j,k in cyclic order)
$ \vec{C}=\vec{A}\times \vec{B}=\sum_{i,j,k}^{}\hat{e_{i}}\epsilon_{ijk}A_{j}B_{k} $
$ =\begin{vmatrix}
\hat{e_{1}} & \hat{e_{2}} & \hat{e_{3}}\\
A_{1} & A_{2} & A_{3} \\
B_{1} & B_{2} & B_{3}
\end{vmatrix}=\hat{e_{1}}\begin{vmatrix}
A_{2} & A_{3} \\
B_{2} & B_{3}
\end{vmatrix}-\hat{e_{2}}\begin{vmatrix}
A_{1} & A_{3} \\
B_{1} & B_{3}
\end{vmatrix}+\hat{e_{3}}\begin{vmatrix}
A_{1} & A_{2} \\
B_{1} & B_{2}
\end{vmatrix} $
26. Properties of Vector Product
$ \vec{A}\times \vec{B}=-\vec{B}\times \vec{A} $
$ \vec{A}\times(\vec{B}\times \vec{C})\neq (\vec{A}\times \vec{B})\times\vec{C} $ in general
$ \vec{A}\cdot (\vec{B}\times \vec{C})=\vec{B}\cdot (\vec{C}\times \vec{A})=\vec{C}\cdot (\vec{A}\times \vec{B})\equiv \vec{A}\vec{B}\vec{C} $
$ \vec{A}\times (\vec{B}\times \vec{C})=(\vec{A}\cdot \vec{C})\vec{B}-(\vec{A}\cdot \vec{B})\vec{C} $
$ (\vec{A}\times\vec{B})\cdot (\vec{C}\times \vec{D})=\vec{A}\cdot [\vec{B}\times (\vec{C}\times\vec{D})]=\vec{A}\cdot [(\vec{B}\cdot \vec{D})\vec{C}-(\vec{B}\cdot \vec{C})\vec{D}]=(\vec{A}\cdot \vec{C})(\vec{B}\cdot \vec{D})-(\vec{A}\cdot \vec{D})(\vec{B}\cdot \vec{C}) $
$ (\vec{A}\times\vec{B})\times(\vec{C}\times \vec{D})=[(\vec{A}\times \vec{B})\cdot\vec{D})]\vec{C}-[(\vec{A}\times \vec{B})\cdot\vec{C})]\vec{D}=(\vec{A}\vec{B}\vec{D})\vec{C}-(\vec{A}\vec{B}\vec{C})\vec{D}=(\vec{A}\vec{C}\vec{D})\vec{B}-(\vec{B}\vec{C}\vec{D})\vec{A} $
'math for physics > vector calculus' 카테고리의 다른 글
| Vector Calculus (12) - Velocity, Acceleration (0) | 2021.07.27 |
|---|---|
| Vector Calculus (11) - Differentiation (0) | 2021.07.26 |
| Vector Calculus (9) - Position Vector, Unit Vector (0) | 2021.07.22 |
| Vector Calculus (8) - Scalar Product (0) | 2021.07.21 |
| Vector Calculus (7) - Definitions and Operations of a Scalar and a Vector (0) | 2021.07.20 |