29. Rectangular Coordinate
Position: $ \vec{r}=\vec{r}(t) $
Velocity: $ \vec{v}\equiv \frac{d\vec{r}}{dt}=\dot{\vec{r}} $
Acceleration: $ \vec{a}\equiv \frac{d\vec{v}}{dt}=\frac{d^{2}\vec{r}}{dt^{2}}=\ddot{\vec{r}} $
Rectangular Coordinates (Unit Vector가 시간에 대한 상수)
Position: $ \vec{r}=x_{1}\hat{e_{1}}+x_{2}\hat{e_{2}}+x_{3}\hat{e_{3}}=\sum_{i}^{}x_{i}\hat{e_{i}} $
Velocity: $ \vec{v}=\dot{\vec{r}}=\sum_{i}^{}\dot{x_{i}}\hat{e_{i}}=\sum_{i}^{}\frac{dx_{i}}{dt}\hat{e_{i}} $
Acceleration: $ \vec{a}=\dot{\vec{v}}=\ddot{\vec{r}}=\sum_{i}^{}\ddot{x_{i}}\hat{e_{i}}=\sum_{i}^{}\frac{d^{2}x_{i}}{dt^{2}}\hat{e_{i}} $
30. Plane Polar Coordinate
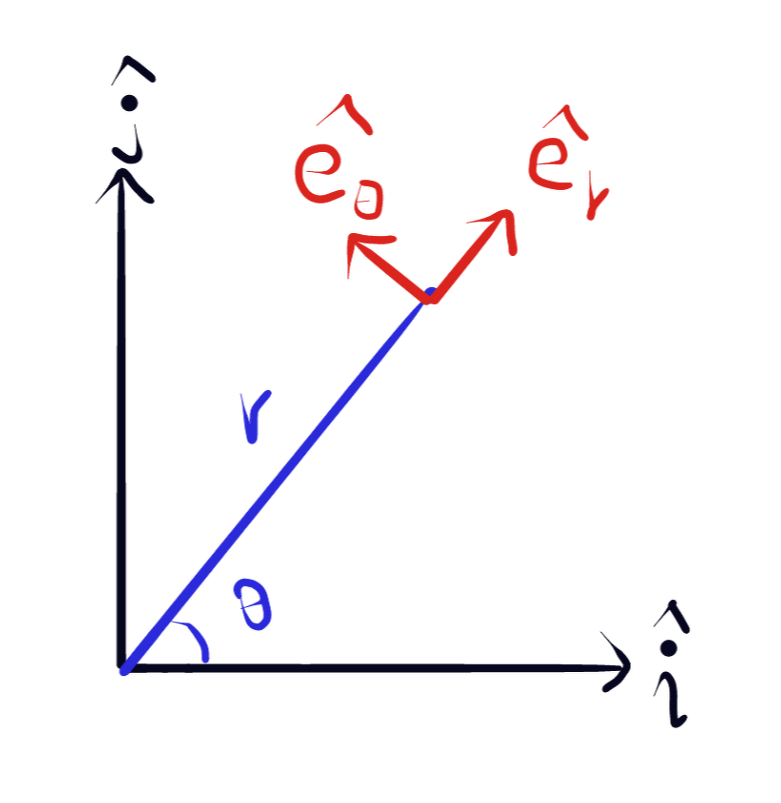
$ \vec{r}=x\hat{i}+y\hat{j}=r\cos \Theta \hat{i}+r\sin \Theta \hat{j} $
$ \hat{e_{r}}=\cos \Theta \hat{i}+\sin \Theta \hat{j} $
$ \hat{e_{\Theta }}=-\sin \Theta \hat{i}+\cos \Theta \hat{j} $
$ \dot{\hat{e_{r}}}=\dot{\Theta }\hat{e_{\Theta }} $
$ \dot{\hat{e_{\Theta }}}=-\dot{\Theta }\hat{e_{r}} $
$ \vec{v}=\dot{r}\hat{e_{r}}+r\dot{\Theta }\hat{e_{\Theta }} $
$ \vec{a}=(\ddot{r}-r\dot{\Theta }^{2})\hat{e_{r}}+(r\ddot{\Theta }+2\dot{r}\dot{\Theta })\hat{e_{\Theta }} $
31. Cylindrical Coordinate

(Plane Polar Coordinate에서 z-axis만 추가)
$ \vec{r}=r\cos \Theta \hat{e_{1}}+r\sin \Theta \hat{e_{2}}+z\hat{e_{3}} $
$ \vec{v}=\dot{r}\hat{e_{r}}+r\dot{\Theta }\hat{e_{\Theta }}+\dot{z}\hat{e_{3}} $
$ \vec{a}=(\ddot{r}-r\dot{\Theta }^{2})\hat{e_{r}}+(r\ddot{\Theta }+2\dot{r}\dot{\Theta })\hat{e_{\Theta }}+\ddot{z}\hat{e_{3}} $
32. Spherical Coordinate
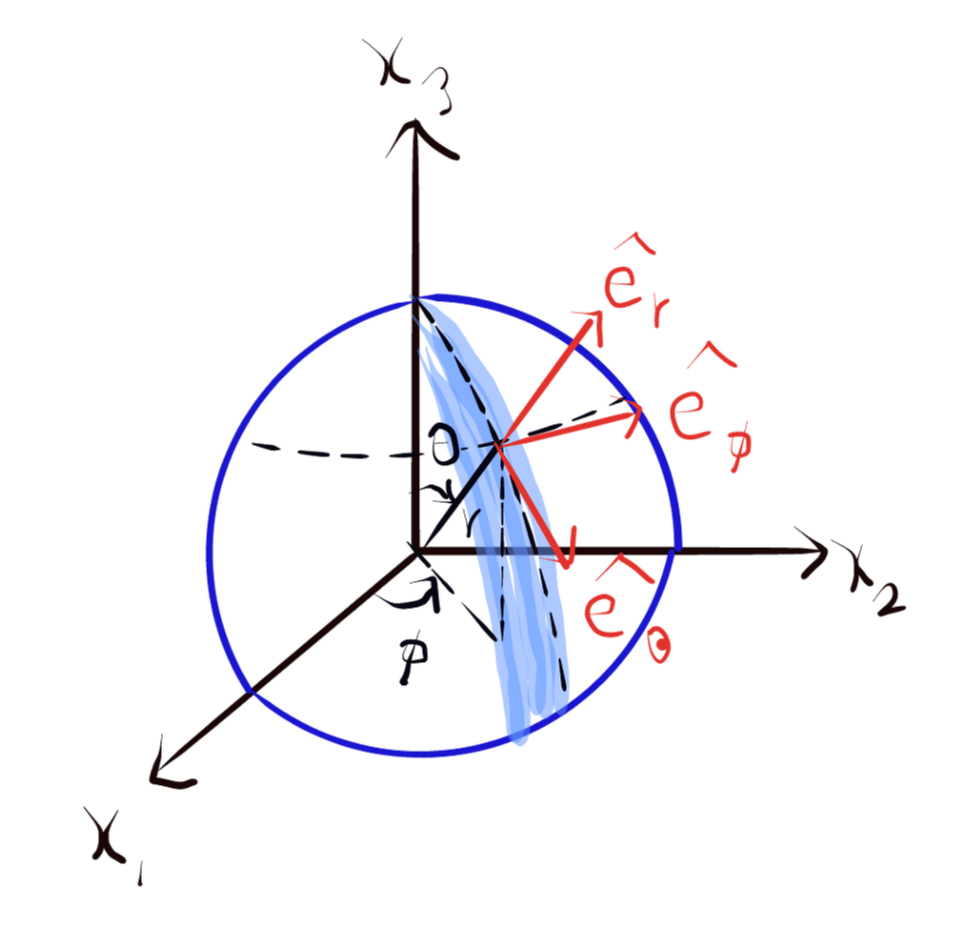
$ \vec{r}=r\sin \Theta \cos \phi \hat{e_{1}}+r\sin \Theta \sin \phi \hat{e_{2}}+r\cos \Theta \hat{e_{3}} $
$ \hat{e_{r}}=\sin \Theta \cos \phi \hat{e_{1}}+\sin \Theta \sin \phi \hat{e_{2}}+\cos \Theta \hat{e_{3}} $
$ \hat{e_{\Theta }}=\cos \Theta \cos \phi \hat{e_{1}}+\cos \Theta \sin \phi \hat{e_{2}}-\sin \Theta \hat{e_{3}} $
$ \hat{e_{\phi }}=-\sin \phi \hat{e_{1}}+\cos \phi \hat{e_{2}} $
$ \vec{v}=\dot{r}\hat{e_{r}}+r\dot{\Theta }\hat{e_{\Theta }}+r\sin \Theta \dot{\phi }\hat{e_{\phi }} $
$ \vec{a}=(\ddot{r}-r\dot{\Theta }^{2}-r\dot{\phi ^{2}}\sin ^{2}\Theta )\hat{e_{r}}+(2\dot{r}\dot{\Theta }+r\ddot{\Theta }-r\dot{\phi }^{2}\sin \Theta \cos \Theta )\hat{e_{\Theta }}+(2r\dot{\Theta }\dot{\phi }+2\dot{r}\dot{\phi }\sin \Theta +r\ddot{\phi }\sin \Theta )\hat{e_{\phi }} $
'math for physics > vector calculus' 카테고리의 다른 글
| Vector Calculus (14) Gradient (0) | 2021.07.30 |
|---|---|
| Vector Calculus (13) - Angular Velocity (0) | 2021.07.28 |
| Vector Calculus (11) - Differentiation (0) | 2021.07.26 |
| Vector Calculus (10) - Vector Product (0) | 2021.07.23 |
| Vector Calculus (9) - Position Vector, Unit Vector (0) | 2021.07.22 |