27. Differentiation of Scalar Function
Scalar Function $ \phi =\phi (s) $
in the $ x_{i},x_{i}' $ coordinates, $ \phi =\phi ', s=s' \Rightarrow d\phi =d\phi ', ds=ds' $
$ \frac{d\phi }{ds}=\frac{d\phi '}{ds'}=(\frac{d\phi }{ds})' $
28. Differentiationn of Vector Function
Vector Function $ \vec{A} $ w.r.t. a scalar S
$ A_{i}'=\sum_{j}^{}\lambda _{ij}A_{j} $
$ \frac{dA_{i}'}{ds'}=\frac{d}{ds'}\sum_{j}^{}\lambda _{ij}A_{j}=\sum_{j}^{}\lambda _{ij}\frac{dA_{j}}{ds'}=\sum_{j}^{}\lambda _{ij}\frac{dA_{j}}{ds} (s=s') $
$ \frac{dA_{j}}{ds} $: components of a vector (=$ \frac{d\vec{A}}{ds} $)
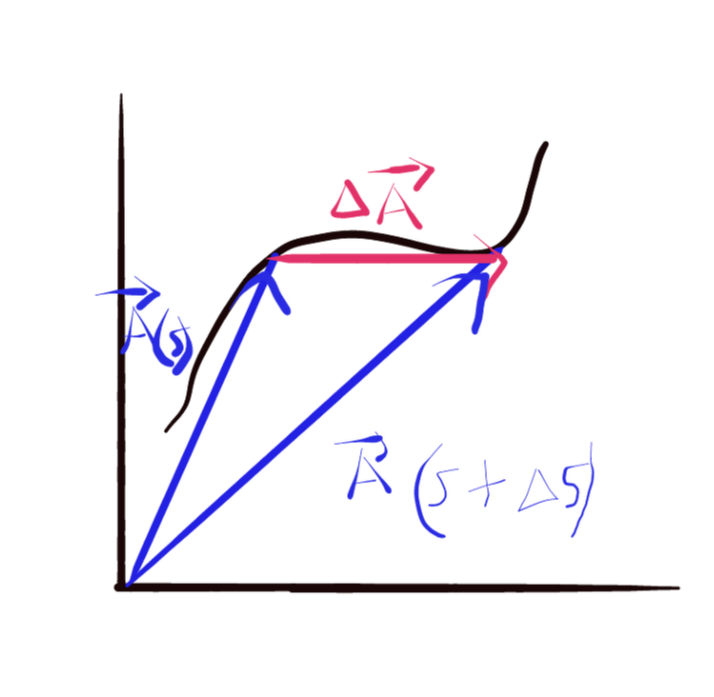
$ \Rightarrow \frac{d\vec{A}}{ds}=\lim_{\Delta s\rightarrow 0}\frac{\Delta \vec{A}}{\Delta s}=\lim_{\Delta s\rightarrow 0}\frac{\vec{A}(s+\Delta s)-\vec{A}(s)}{\Delta s} $
$ \frac{d}{ds}(\vec{A}+\vec{B})=\frac{d\vec{A}}{ds}+\frac{d\vec{B}}{ds} $
$ \frac{d}{ds}(\vec{A}\cdot \vec{B})=\frac{d\vec{A}}{ds}\cdot\vec{B} +\vec{A}\cdot \frac{d\vec{B}}{ds} $
$ \frac{d}{ds}(\vec{A}\times \vec{B})=\frac{d\vec{A}}{ds}\times\vec{B}+\vec{A}\times \frac{d\vec{B}}{ds} $
$ \frac{d}{ds}(\phi \vec{A})=\frac{d\phi }{ds}\vec{A}+\phi \frac{d\vec{A}}{ds} $
'math for physics > vector calculus' 카테고리의 다른 글
| Vector Calculus (13) - Angular Velocity (0) | 2021.07.28 |
|---|---|
| Vector Calculus (12) - Velocity, Acceleration (0) | 2021.07.27 |
| Vector Calculus (10) - Vector Product (0) | 2021.07.23 |
| Vector Calculus (9) - Position Vector, Unit Vector (0) | 2021.07.22 |
| Vector Calculus (8) - Scalar Product (0) | 2021.07.21 |